连续复利利率的计算

什么是连续复利

当m=1时所对应的利率被称为等值年利率（equivalent annual interest rate）。当m趋于正无穷大（m→＋∞）时，就称为连续复利（continuous compounding），对应的利率称为“连续复利率”(continuously compounded rate)。

FV = \displaystyle \lim_{m \to +\infty} A(1+{{R}\over{m}})^{mn} = Ae^{Rn}

等价关系

连续复利利率与每年m次复利利率的等价关系式。

R_c=m\times\ln(1+{{R_m}\over{m}})

R_m=m\times(e^{{R_c} /{m}}-1)

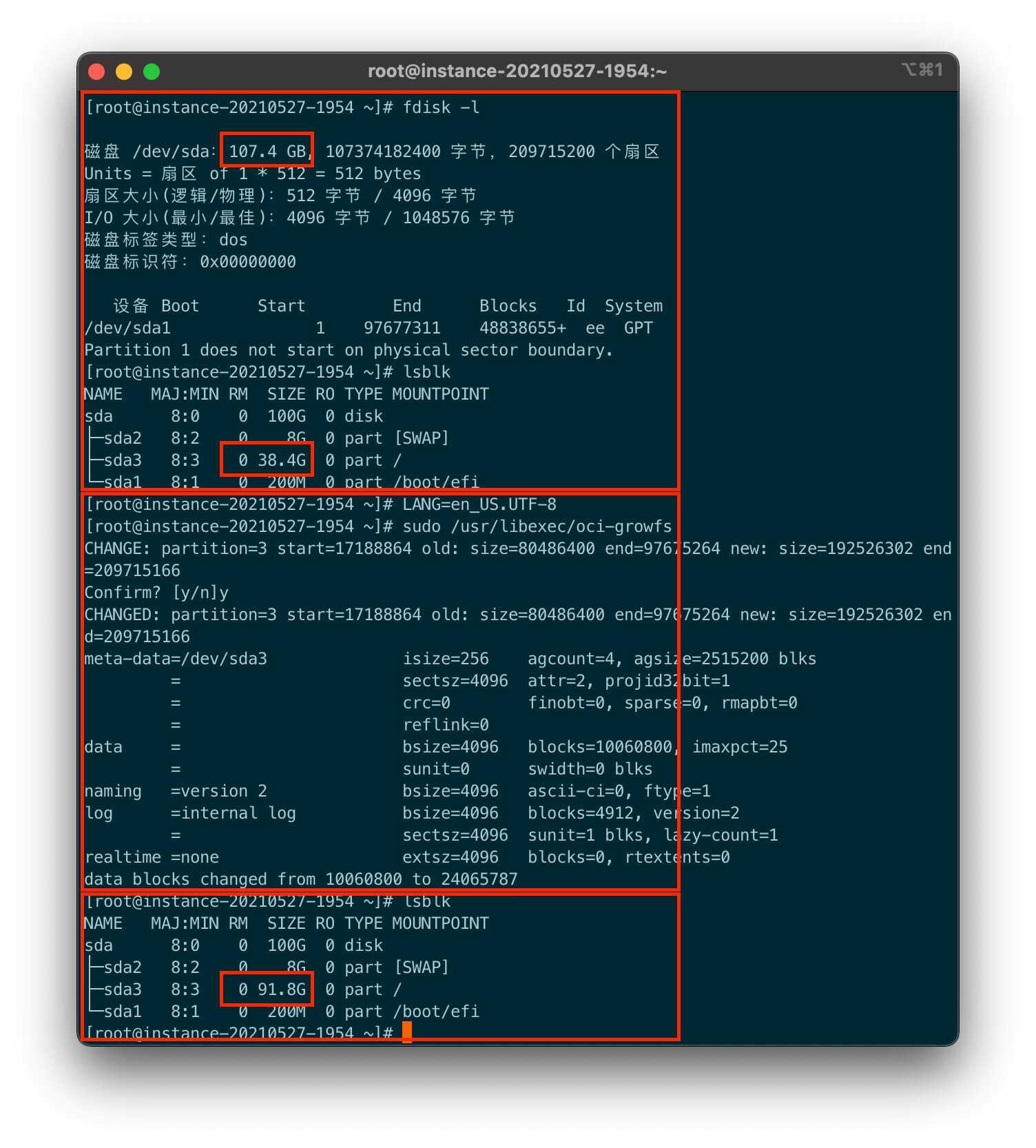
转换代码

def Rc(Rm,m):
    '''
    构建已知复利频次和对应的复利利率，计算等价连续复利利率的函数。
    Rm: 复利频次m的复利利率；
    m: 复利频次。
    '''
    import numpy as np 
    return m*np.log(1+Rm/m)

def Rm(Rc,m):
    '''
    构建已知复利频次和连续复利利率，计算等价的对应复利m次复利利率函数。
    Rc: 连续复复利利率；
    m: 复利频次。
    '''
    import numpy as np 
    return m*(np.exp(Rc/m)-1)

例题1 假定G商业银行对外的利率报价是5%，按季度复利，计算相对应的连续复利利率。等价的连续复利利率等于：

Rc(0.05,4)

结果为：0.04969007999422844

例题2 假设H商业银行对外的利率报价是6%，该利率是连续复利利率，计算等价的每月复利利率。等价的每月复利利率等于：

Rm(0.06,12)

结果为：0.060150250312811515